side 1

Bevægelse og differentialregning

Fra et projekt i fysik og matematik for 2.g matematisk naturvidenskabelig linie.

Noter i matematik for 2yw MA.          18-11-04.
 
Indhold
  0. Indledning   side  1
  1. Stedfunktion, hastighedsfunktion og accelerationsfunktion side  2
  2. Grafisk og numerisk differentiation side  3
  3. Stamfunktion og areal side  8
  4. Konklusion om den grafiske sammenhæng mellem  s, v og a side 11
  5. Eulers metode. Numerisk løsning af en differentialligning. side 12
       
0. Indledning
0.1. Forudsætning
  Forud for projektugen har holdet læst følgende om differentialregning:
  Kapitel  "XI. Differentialkvotient"  i  "Grundbog i Matematik"
Kapitel  "VII. Differentialregning."  i  "Højniveaumatematik 1"
      siderne  126, 127, 128, 129,   150, 151, 152, 153
 
0.2. Arbejdet i projektgruppen
  Ved dagens begyndelse mødes projektgruppens medlemmer og delagtiggør hinanden
i resultatet af det arbejde som de hver for sig har udført hjemme siden sidst. Der vælges
en referent som det påhviler at udfylde dagens blad i projektdagbogen i projektmappen.
Resultatet af hjemmearbejdet beskrives kortfattet i projektdagbogen og det sammenlignes
med det der blev aftalt om hjemmearbejde i slutningen af det foregående møde.
  I løbet af dagen arbejder projektgruppens medlemmer ifølge dagens program. Beslut-
ninger der bliver truffet i dagens løb og andre oplysninger der er relevante for gruppens
arbejde indskrives i projektdagbogen.
  Ved skoledagens slutning mødes projektgruppens medlemmer og aftaler hvad der skal
arbejdes med hjemme indtil næste møde. Aftalen indskrives kortfattet i projektdagbogen.
         
0.3. Projektrapportens matematikdel
  Teksten i rapporten skal være sammenhængende og let forståelig og skal indeholde besvarelser
af opgaver fra disse noter.
  Hvilke opgaver der skal inddrages aftales i gruppen og med P.Aa.
  Det bedste resultat for både den enkelte og for gruppens rapport fås igennem en passende
kombination af individuelt arbejde og arbejde i gruppen.
Således er det meget vigtigt at hvert gruppemedlem arbejder individuelt med hver opgave
selvom gruppen kun bruger en af opgaveløsningerne i rapporten.
Og det er vigtigt at gruppen arbejder sammen om den mere overordnede udformning af rapporten.
Herunder rapportens disposition og udseende og valg af hvilke opgaveløsninger der skal bruges.
side 2
1. Stedfunktion, hastighedsfunktion og accelerationsfunktion TOP
Opgave 1.
  Forklar hvad der menes med begreberne stedfunktion, hastighedsfunktion og accelerationsfunktion
og forklar hvilken sammenhæng der er mellem dem.
Prøv at give forklaringerne både i hverdagssprog og i et mere præcist sprog.
Opgave 2.
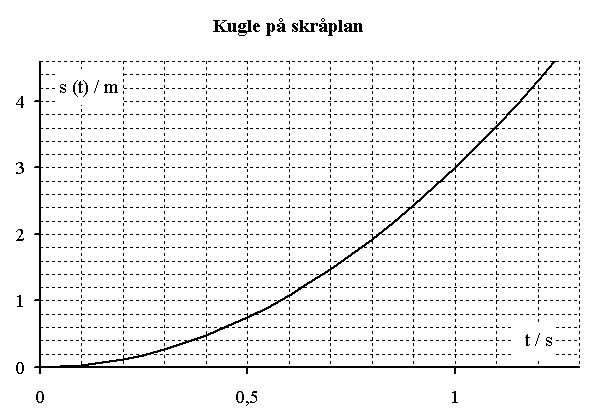
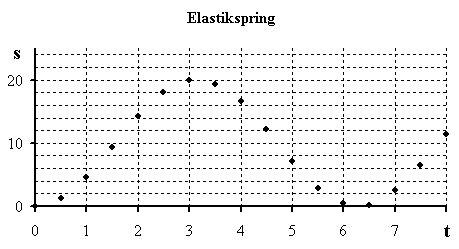
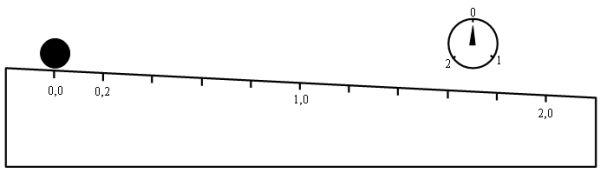
  En kugle ruller ned ad et skråplan.
 
  KLIK PÅ TEGNINGEN FOR AT SE EN PRÆSENTATION
  KLIK HER FOR AT SE PRÆSENTATIONEN SOM HTML
  Kuglens "sted" er fastlagt ved skråplanets målestok.
I opgaven skal der ikke regnes med enheder, men det kunne godt passe med  s  regnet i meter
og t regnet i sekunder.
  Stedfunktionen for kuglen er givet ved:
    s(t) = 0,25 ∙ t2
  i tidsrummrt  0  til  3.
  a) Tegn grafen for  s(t)
  b) Bestem hastighedsfunktionen  v(t)  og accelerationsfunktionen  a(t)
  c) Tegn graferne for  v(t)  og  a(t). Gerne i samme koordinatsystem som  s(t).
Opgave 3.
  En partikel bevæger sig langs en ret linie med stedfunktionen  s  givet ved:
    s(t) = 0,02 ∙ t3  -  0,3 ∙ t2  +  t  +  2
  i tisdrummet  0  til  10. Der ses igen bort fra enhederne.
  a) Bestem hastighedsfunktionen og accelerationsfunktionen.
  b) Tegn graferne for  s(t),  v(t)  og  a(t)  i samme koordinatsystem
  c) Gør rede for hvad der er særlig grund til at lægge mærke til
når man sammenligner graferne for  s(t),  v(t)  og  a(t).
         
         
TOP
side 3
2. Grafisk og numerisk differentiation.
2.1 Bestemmelse af den afledede funktion ud fra funktionens graf. Grafisk differentiation.
Opgave 4.
  JÆVN BEVÆGELSE.
  En puk glider hen over isen med stedfunktionen  s(t)  givet ved sin graf:
 
  a) Bestem hastighedsfunktionen (hastigheden) og accelerationsfunktionen (accelerationen).
  b) Tegn graferne for  s(t), v(t)  og  a(t)  i samme koordinatsystem. Uden enheder.
    Jeg har taget enheder med på tegningen, men det er egentlig forkert.
 
 
TOP
side 4
Opgave 5. TOP
  JÆVNT VOKSENDE BEVÆGELSE.
  En kugle ruller ned ad et skråplan.  (Et andet skråplan end det i opgave 2).
  Kuglens stedfunktion  s(t)  er givet ved sin graf:
 
 

KLIK PÅ BILLEDET FOR AT SE EN FORSTØRRET GRAF
  a) Bestem kuglens hastighed for  t =  0,3;  0,5;  0,7;  0,9;  1,1  ved at bestemme hældnings-
koefficienterne for tangenterne i de tilsvarende punkter på grafen. (Vi ser bort fra enheder).
Brug gerne en udskrift af det forstørrede billede.
  b) Indsæt de fundne hastigheder i et koordinatsystem og tegn på det grundlag grafen for
hastighedsfunktionen  v(t).  Brug lineær regression.
  c) Bestem accelerationsfunktionen  a(t)  ud fra grafen for hastighedsfunktionen.
  d) Tegn grafen for accelerationsfunktionen og sammenlign graferne for  s(t),  v(t)  og  a(t).
         
         
TOP
side 5
Opgave 6. TOP
  BILTUR EFTER MORGENBRØD.
  En søndag formiddag sætter hr. Andersen sig i sin bil for at køre efter morgenbrød.
Der er først et stykke på landevej og så efter et lyskryds et stykke vej inde i byen
inden han når frem til bageren.
Han er lidt sent på den så han accelererer bilen så stærkt som dens motor kan klare.
Desværre kommer han straks til at køre bag ved en lastbil som kørte lidt langsommere end han
selv havde tænkt sig at køre.
Lastbilen drejer ind i en indkørsel lige før lyskrydset.
Derfor opdager han først i sidste øjeblik at der er rødt lys.
Han bremser op så hurtigt han kan og får derefter nogle få sekunder at sunde sig i
inden der bliver grønt.
Nu har han fået lyst til at tage den lidt med ro så han sætter roligt bilen op i fart,
han kører roligt gennem byen (bag en traktor) og han standser roligt op ved bagerbutikken.
Her kan du se grafen for stedfunktionen for hr. Andersens tur til bageren.
 
 

KLIK PÅ BILLEDET FOR AT SE EN FORSTØRRET GRAF
  Det kan antages at alle bilens (fire) accelerationer er sket med konstant acceleration.
  a) Beregn først bilens hastigheder i de tre tidsrum hvor hastigheden var konstant.
Det var: på landevejen, ved det røde lys og i byen.
Tegn dernæst grafen for hastighedsfunktionen  v(t) .
  b) Bestem accelerationsfunktionen  a(t)  og tegn dens graf.
Sammenlign graferne for  s(t),  v(t)  og  a(t).
         
         
TOP
side 6
2.2 Bestemmelse af den afledede funktion ud fra en tabel over funktionsværdier.
Numerisk differentiation.
Opgave 7.
  LODRET KAST.
  En legetøjskanon skyder en kugle lodret op.
Kuglen vil så bevæge sig op langs en lodret linie, nå til det højeste punkt,
vende tilbage langs den lodrette linie og ende i kanonens løb.
Kuglens stedfunktion (dens højde over kanonens munding)
er vist i tabellen til højre.
Nedenfor er vist tabellens punkter indsat i et koordinatsystem.
Stedfunktionens graf er en "blød" kurve igennem disse punkter.
t / s s / m
0,0 0,000
0,1 0,551
0,2 1,004
0,3 1,358
0,4 1,614
0,5 1,773
0,6 1,832
0,7 1,794
0,8 1,658
0,9 1,423
1,0 1,090
1,1 0,659
1,2 0,130
 
  a) Til tiden 0,8 er kuglen åbenbart på vej ned igen.
Kuglens hastighed for t = 0,8 er  v(0,8) = s'(0,8).
Ved numerisk differentiation kan en god tilnærmelse til  s'(0,8)  findes ved at udregne
hældningskoefficienten for sekanten igennem "nabopunkterne" til  (0,8 ;  s(0,8)).
Se tegningen.
Beregn på denne måde  v(0,8) = s'(0,8).
  b) Beregn  v(t)  for  t = 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1,0; 1,1;
Brug f.eks. regneark. Så er det mere overkommeligt.
Indsæt punkterne i et  (t; v) koordinatsystem og tegn grafen for  v(t).
  c) Bestem på lignende måde accelerationsfunktionen  a(t).
Tegn grafen for  a(t)  i samme koordinatsystem som grafen for  v(t).
  d) Aflæs på grafen for  v(t)  kuglens starthastighed, (også kaldet mundingshastigheden)
og aflæs det tidspunkt hvor kuglen er højest oppe.
         
         
TOP
side 7
Opgave 8
  ELASTIKSPRING
I et elastikspring bevæges et menneske op og ned et antal gange fastgjort til
den ene ende af en elastik der i den anden ende er fastgjort tilstrækkeligt højt
oppe til at mennesket holdes fri af jorden.
I det elastikspring der her betragtes starter bevægelsen med at mennesket står
på jorden og trækkes op af en i forvejen udspændt elastik.
Menneskets stedfunktion  s(t)  som er højden over jordoverfladen er vist i
tabelform til højre. Nedenfor ses punkterne sat ind i koordinatsystem.
t / s s / m
0,0 0,00
0,5 1,22
1,0 4,60
1,5 9,29
2,0 14,16
2,5 18,01
3,0 19,90
3,5 19,36
4,0 16,54
4,5 12,11
5,0 7,16
5,5 2,91
6,0 0,40
6,5 0,23
7,0 2,46
7,5 6,53
8,0 11,46
 
  KLIK HER FOR AT SE TABELLEN I REGNEARK
  KLIK HER FOR AT SE ET FORSTØRRET KOORDINATSYSTEM
  a) Bestem ved hjælp af numerisk differentiation en tabel over tilnærmede værdier for
hastighedsfunktionen  v(t).
Gør det gerne ved at udvide det regneark der er link til ovenfor.
  b) Bestem på grundlag af hastighedsværdierne en tabel over tilnærmede værdier for
accelerationsfunktionen  a(t).
Gør det gerne ved at udvide det regneark der blev udvidet under a).
  c) Tegn med "bløde" kurver graferne for  s(t),  v(t)  og  a(t)  i samme koordinatsystem.
Brug gerne det forstørrede koordinatsystem der er link til ovenfor og hvor  s(t)  punkterne
allerede er indsat.
  d) Bestem ved at betragte  s - grafen  menneskets største højde over jordoverfladen.
  e) Bestem ved at betragte  v - grafen 
   -   tidspunktet for den største højde (se efter  v = 0),
   -   tidspunkterne for den mindste højde (se efter  v = 0),
   -   svingningstiden, tiden for en hel svingning,
   -   den største værdi for hastigheden
   -   et skøn over hastigheden til tiden  t = 0.
  f) Bestem ved at betragte  a - grafen,
   -   tidspunkterne for de største hastigheder (se efter  a = 0),
   -   den største værdi for accelerationen.
         
TOP
side 8
3. Stamfunktion og areal.
3.1. Stamfunktion.
Betragt to funktioner  F(x)  og  f(x)  hvor F'(x) = f(x);  f(x) er altså den afledede funktion til  F(x).
Omvendt siges  F(x)  at være en stamfunktion til  f(x).
F'(x) = f(x)  kaldes stamfunktionsprøven.
Det er den prøve som F(x) skal bestå for at fortjene titel af stamfunktion til f(x).
Hvis f.eks. F(x) = x3  og  f(x) = 3∙x2  så er  F'(x) = f(x).
Altså er  f(x) = 3∙x2  den afledede funktion til  F(x) = x3 
og  F(x) = x3  er en stamfunktion til  f(x) = 3∙x2 .
Det kan ofte være praktisk at navngive stamfunktioner med store bogstaver.
Således at f.eks. funktionerne  f,  g  og  h  har stamfunktioner  F,  G  og  H.
Denne måde at navngive stamfunktioner på er imidlertid ikke obligatorisk.
Opgave 9.
  Der er givet to funktioner   f(x) = x2 + x - 1   og   g(x) = 2∙x + 1 .
  a) Hvilken af de to funktioner er den afledede funktion til den anden?
  b) Hvilken af de to funktioner er en stamfunktion til den anden
Opgave 10
  Betragt stedfunktionen  s(t),  hastighedsfunktionen  v(t)  og accelerationsfunktionen  a(t)
for en bestemt partikelbevægelse.
  a) Hvilken af funktionerne  s(t)  og  v(t)  er den afledede funktion til den anden?
  b) Hvilken af funktionerne  s(t)  og  v(t)  er en stamfunktion til den anden?
  c) Hvilken af funktionerne  v(t)  og  a(t)  er en stamfunktion til den anden?
Opgave 11
  En bevægelse for en partikel har hastighedsfunktionen  v(t) = 2∙t - 1.
  a) Bestem bevægelsens accelerationsfunktion  a(t).
  b) Hvilke af de følgende funktioner kan være stedfunktioner til bevægelsen ?
s1(t) = t2 - t ,  s2(t) = t2 - 1 ,  s3(t) = t2 - t + 7 ,  s4(t) = 2∙t2 - 2∙t ,  s5(t) = t2 - t + π .
Opgave 12.
  En bevægelse for en partikel har hastighedsfunktionen  v(t) = 0,6∙t + 2.
  a) Bestem bevægelsens accelerationsfunktion  a(t).
  b) Bestem alle de mulige stedfunktioner for bevægelsen.
  c) Bestem stedfunktionen  s(t)  når det vides at  s(0) = 3,5.
Opgave 13.
  En bold bevæger sig i tidsrummet fra  0  til  1,1  med accelerationen  a =  -9,82.
Startbetingelserne er  s(0) = 2  og  v(0) = 6,27.
  a) Bestem hastighedsfunktionen  v(t).
  b) Bestem stedfunktionen  s(t).
  c) Tegn graferne for  s(t)  og  v(t)  og bestem maksimum for  s. 
Beregn  s(1,1).
     
 
side 9
3.2. Areal. TOP
Opgave 14.
  En bevægelse for en partikel har stedfunktionen  s(t) = 0,3∙t2 .
  a) Gør rede for at bevægelsens hastighedsfunktion er  v(t) = 0,6∙t .
  Nedenfor ses grafen for  v(t)  med en skraveret trekant indtegnet
mellem  t-aksen og grafen.
Trekantens vinkelspidser er  (0, 0),  (4, 0)  og  (4, v(4)).
 
  b) Beregn trekantens areal.  Sammenlign dette med  s(4).
  Nedenfor er en ny skraveret trekant indtegnet under grafen for  v(t).
Nu med vinkelspidserne  (0, 0),  (t, 0)  og  (t, v(t)).
 
  c) Beregn trekantens areal udtrykt ved  t.
  d) Sammenlign udtrykket for trekantens areal med  s(t)  (en stamfunktionen til  v(t)).
Hermed er der antydet en ny sammenhæng mellem  s(t)  og  v(t).
Hvad er det for en sammenhæng?
         
         
side 10
Opgave 15. TOP
  En bevægelse for en partikel har stedfunktionen  s(t) = -0,15∙t2 + 5∙t + 0,7 .
  a) Bestem  s(2)  og  s(7)    
  b) Hvor langt et stykke  Δs  har partiklen bevæget sig i tidsrummet  2  til  7 ?
  c) Gør rede for at bevægelsens hastighedsfunktion er  v(t) = -0,3∙t + 5
  Nedenfor ses grafen for  v(t).
En del af området mellem  t-aksen  og grafen er skraveret.
Det er den del af området der "svarer til" tidsrummet fra  2  til  7.
Det skraverede område er et trapez med vinkelspidserne 
(2, 0),  (7, 0),  (7, v(7))  og  (2, v(2)).
   
  d) Bestem  v(2)  og  v(7)  og beregn trapezets areal.    
  e) Sammenlign resultaterne fra  b)  og  d).
Kan du skimte en mulig generalisering?
   
         
         
side 11
Opgave 16 TOP
  En bevægelse for en partikel har stedfunktionen  s(t) = a∙t2 + v0∙t + s0 .
  a) Bestem Δs = s(t2) - s(t1)  udtrykt ved  t1 ,  t2 ,  a  og  v0 .  
  b) Gør rede for at bevægelsens hastighedsfunktion er  v(t) = 2∙a∙t + v0 .
  Nedenfor ses et eksempel på en graf for en sådan hastighedsfunktion  v(t) = 2at + v0 .
En del af området mellem  t-aksen og grafen er skraveret.
Det er den del af området der svarer til tidsrummet fra  t1  til  t2 .
   
  c) Angiv vinkelspidserne for den skraverede firkant.
  d) Bestem firkantens areal udtrykt ved  t1 ,  t2 ,  a  og  v0 .
  e) Gør rede for at resultaterne i  a)  og  d)  er lig med hinanden.
4: Konklusion om den grafiske sammenhæng mellem  s(t),  v(t)  og  a(t) TOP
Nu har vi set at  hastigheden  v  kan aflæses som hældningskoefficienten for en tangent til grafen
for stedfunktionen  s(t).
Og vi har set at accelerationen  a  kan aflæses som hældningskoefficienten for en tangent til grafen
for hastighedsfunktionen  v(t).
Vi har fået en antydning af hvordan tilvæksten  Δs  for stedfunktionen kan aflæses som et areal
under grafen for hastighedsfunktionen.
Og en antydning af hvordan tilvæksten  Δv  for hastighedsfunktionen kan aflæses som et areal
under grafen for accelerationsfunktionen.
Disse sammenhænge er søgt illustreret på nedenstående tegning.
 
side 12
5. Eulers metode. Numerisk løsning af en differentialligning. TOP
Eksempel  
  En tønde med væske tømmes ved at væsken strømmer
ud gennem et hul i bunden.
Vi vil bestemme den tid der går inden tønden er tømt.
Derfor vil vi undersøge væskeoverfladens bevægelse.
Som stedfunktion  s(t)  vælger vi overfladens højde
over tøndens bund.
Tøndens diameter er  0,28 m,  hullets diameter er
0,015 m og start-højden  s(0)  =  0,40 m.
 

KLIK PÅ BILLEDET FOR AT SE EN PRÆSENTATION AF TØMNINGEN
KLIK HER FOR AT SE HTML-UDGAVE AF PRÆSENTATONEN
  I dette tilfælde kender vi hverken  s(t),  v(t)  eller  a(t).
Så vi kan ikke bruge nogen af de metoder som vi har arbejdet med i det foregående.
Vi kan dog godt sige noget om  v(t).
Overfladens hastighed må jo afhænge af overfladens højde over bunden.
Fordi: jo mindre overfladehøjde jo mindre væsketryk nede ved hullet
d.v.s. jo langsommere udstrømning og derfor jo langsommere overfladehastighed.
Ud fra dimensionerne af tønde og hul og nogle enkle energibetragtninger kan man nå frem til
følgende model for bevægelsen:   
v(t)  =  s'(t)  =  -0,0125∙(s(t))½ 
  I denne ligning er den ubekendte størrelse funktionen  s(t).
Ligning kaldes en differentialligning fordi den indeholder den afledede funktion til s(t).
Vi vil benytte Eulers metode til at løse ligningen numerisk og dermed løse vores problem:
at bestemme tømningstiden.
I Eulers metode udnyttes at:
  differenskvotienten  Δs/Δt  er ca. lig med differentialkvotienten  s'(t)  når  Δt  er tæt på 0.
   Δs / Δt  ~  s'(t)    <=>    Δs  ~  s'(t)∙Δt       når   Δt  ~ 0.
  Med en bestemt værdi for  Δt  ser vi på disse  t-værdier:
  t0 = 0,  t1 = Δt,  t2 = 2∙Δt, ... ,ti = i∙Δt, ...
  For at bestemme de tilsvarende (tilnærmede) funktionsværdier fås:
  Δs = s(t1) - s(t0) ~ s'(t0)∙Δt    <=>    s(t1) ~ s(t0) + s'(t0)∙Δt
  Generelt fås:
  s(ti+1)  ~  s(ti) + s'(ti)∙Δt
  I vores tilfælde med tømning af en tønde fås:
  s(ti+1)   ~   s(ti) - 0,0125∙(s(ti))½∙Δt
Opgave 17.
  a) Sæt  Δt = 25  og bestem  s(25)  og  s(50)
  b) Bestem den tilnærmede værdi for tømningstiden med denne værdi for  Δt
  c) Prøv med andre (mindre) værdier for  Δt. Hvad er gruppens bud på tømningstiden.
         
  TOP