Skolens regnearkprogram

På alle skolens computere findes regnearkprogrammet Excel. Med et regnearkprogram kan du bl.a. analyse små og større talmængder, lave grafer og små og store beregningsprogrammer. Regneark kan du have brug for i alle fag, hvor der regnes og/eller opsamles og bearbejdes data. 

Som et tilbud til elever, der ikke hjemme har tekstbehandlings- og/eller regnearkprogrammer af nyere dato installeret udleveres en CD med hele StarOffice-programpakken gratis til elever, der beder om det på datavejlederkontoret.

Introducerende vejledning til de mest basale funktioner i programmet Excel 2003
Svarende, stort set, til færdighedsmålene efter 1.g i skolens IT-kompetenceplan

15 små lektioner her på siden (pt er ikke alle færdige):

1. Start programmet

2. Indsæt tal og tekst i celler - brug fyldhåndtaget hvor du kan

3. Formatér celler efter indholdets type

4. Indsæt formler - og skeln mellem relative og absolutte referencer

5. Brug funktioner

6. Sortér data

7. Lav enkle grafiske fremstillinger

8. Arbejd i flere ark

9. Udskriv fra Excel med sidehoved og-fod

10. Integrer mellem Excel og Word

11. Lav lineær regression i grafer

12. Lav tabeller og grafer ud fra funktionsforskrifter

13. Importér data fra forsøg gemt i csv-format (el. tilsvarende)

14. Pivottabeller

15. Chi²-test

1. Start Excel

Start - Programmer - MS Office 2003 - Microsoft Excel 2003.

I eksemplet, som de første punkter i vejledningen her tager udgangspunkt i, skal vi arbejde med data fra en biologiøvelse om osmose. Nogle kartoffelstykker har været badet i sukkeropløsninger med forskellig styrke. Inden og efter badet blev deres længde målt og de blev vejet. Vi skal oprette en tabel med nogle "aflæste data" og derefter have regnearket til at regne nogle "beregnede data" ud v.h.a. formler. Så skal vi have programmet til at anskueliggøre de beregnede data i en graf. Til sidst skal vi se, hvordan man udskriver fra Excel og hvordan man kan flytte elementer fra Excel over i Word til f.eks. rapportbrug og vi skal kigge på nogle af de lidt mere avancerede regnefunktioner i Excel.

2. Indsæt tal og tekst i celler - brug fyldhåndtaget hvor du kan

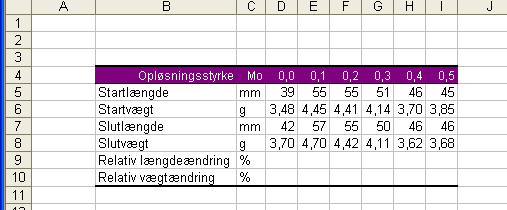
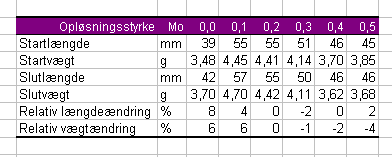
Skemaet skal bestå længst til venstre af en kolonne med betegnelser i tekst for de forskellige størrelser der er aflæst og som skal beregnes. Øverst skal det angives hvilken sukkerkoncentration, der var i de 6 bade. Det er øvelsens såkaldte uafhængige variable, fordi vi selv blandede sukkeropløsningerne og dermed kunne kontrollere dem nøjagtigt. Placér cursoren i en af regnearkets celler, f.eks. B4, og skriv ordet Opløsningsstyrke.

Som det ses er ordet bredere end cellen. Selv om der senere kommer længere ord kan vi godt med det samme tilpasse bredden af kolonnen, så hele ordet kan ses - også når vi skriver noget i nabocellen C4.

Markér kolonnen ved at klikke oppe i B-feltet og vælg Formater - Kolonne - Autotilpas. Straks tilpasses kolonnens bredde det indtastede ords længde:

Gem dit regneark, hvis du ikke allerede har gjort det. Gem jævnligt herefter.

Nu kan vi begynde at udfylde resten af rækken:

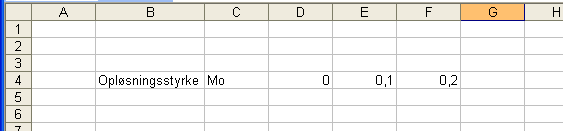
Vi skal op til 0,5 i opløsningsstyrke, og selv om det ikke er et stort arbejde lige her selv at skrive det ind i cellerne én efter én, kan vi godt benytte lejligheden til at kigge på en smart funktion i Excel: Automatisk udfyldning af celler i en række eller en kolonne, hvor udfyldningen er startet og hvor udfyldningen skal følge et bestemt mønster. Som det fremgår er mønstret her, at koncentrationsværdierne "springer" med 0,1 Mo. 

Markér de tre celler med talværdier og placér derefter cursoren på den lille firkant i markeringens nederste højre hjørne, så cursoren bliver korsformet:

Træk markeringsfeltet større mod højre og læg mærke til, hvordan programmet selv "tæller op". Slip når det passer så yderste celle til højre er I4. Voila!

Skemaet udfyldes nu med resten af størrelserne, de tilhørende enheder og værdier. Resten af de aflæste data er de såkaldte afhængige variable, fordi vi jo ikke i detaljer kunne kontrollere kartoffelstumpernes vækst eller skrumpning. Det afhang netop af den uafhængige variabels forskellige værdier. Derfor varierer de ikke systematisk og derfor får vi ikke brug for autoudfyldningen mere, men må selv indskrive alle dataværdierne fra vores øvelsesnoter. Vi laver plads til to rækker med beregnede værdier:

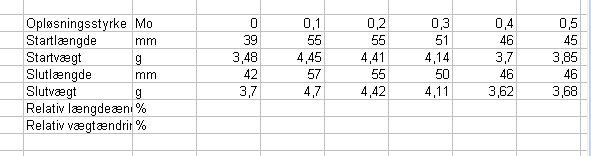
Som det fremgår er betegnelserne for de beregnede størrelser længere end ordet Opløsningsstyrke. Tilpas selv kolonnebredden, så det kommer til at passe.

3. Formatér celler efter indholdets type

I cellerne D8 og E8 er der én decimal efter kommaet og i resten af cellerne til højre herfor er der 2 decimaler. Det ser underligt ud. Blev de to kartoffelstykker vejet på en vægt, der kun kunne måle med 1/10 g´s nøjagtighed og de sidste fire på en vægt med 1/100 g´s nøjagtighed? Faktisk ikke og på øvelsesnotaterne står der også værdierne 3,70 og 4,70 og det er også dét jeg har tastet ind. Hvorfor fjerner programmet så den sidste decimal, når jeg går videre? Hold da op med det!

Problemet er, at vi ikke har fortalt programmet, hvad det er for en datatype vi indtaster, og hvordan det skal behandle dem. Programmet "tænker", at 0´et jo ikke betyder noget beregningsmæssigt, og derfor fjernes det. Men vi vil jo gerne signalere, at vi altså har vejet kartoffelstykket til præcis 3,70 g og ikke "bare" til 3,7g.

Vi kan fortælle programmet, at det er talværdier, der står i cellerne D4 til E10, og at vi vil have 2 decimaler på alle værdier som er målt med 1/100´s nøjagtighed. Da vi ikke vil have to decimaler på mm-værdierne (så gode øjne har vi jo ikke), må vi markere cellerne D6 - I6 og D8 - I8. Det kan gøres ved at markere den ene række først og så holde Ctrl-tasten nede, mens den anden række markeres:

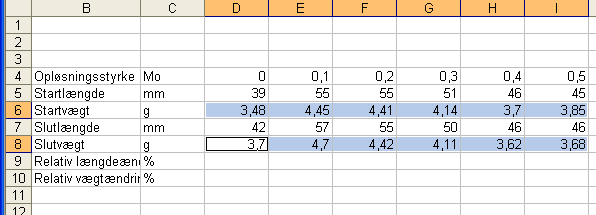
Højreklik et sted i en markeret celle og vælg Formater celler. Flyt Kategorimarkeringen fra Standard til Tal og flyt decimalantallet til 2, hvis det ikke står der allerede:

Kig evt. på fanebladene Kant og Mønstre. Her kan du foretage valg, der får dit skema til at tage sig smart ud. Lad være med at bruge for megen tid her, medmindre du har overskud til det. Klik OK, når du er færdig. Så har vægtværdierne det rigtige antal decimaler:

Opløsningen med styrke 0 har styrken præcis 0,0. Formatér cellerne D4-I4, så det vises rigtigt.

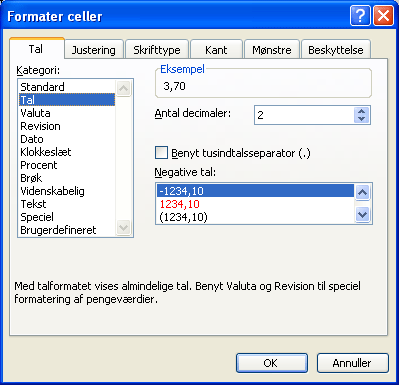
Indholdet i cellerne B4-C10 er tekst og skal behandles sådan i programmet. Det kan f.eks. have betydning, når der skal laves grafer. Markér cellerne - Højreklik - Vælg Formatér celler og flyt markeringen fra Standard til Tekst:

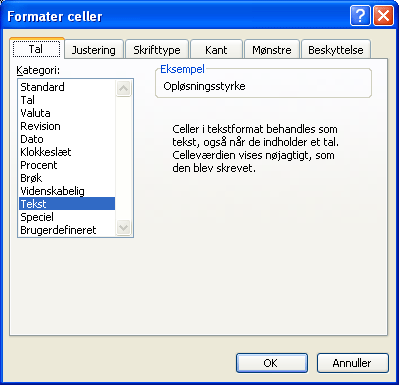
Kig evt. på fanebladene Justering og Skrifttype. Her kan du foretage valg, der får dit skema til at tage sig smart ud. Lad være med at bruge for megen tid her, medmindre du har overskud til det. Klik OK, når du er færdig.

Du kan bruge programmets Autoformatfunktion til at give dit skema et professionelt look. Det kan være meget tidsbesparende i forhold til selv at sidde møjsommeligt at arbejde med rammer, baggrunde og farver, hvis du f.eks. skal bruge dit skema i en rapport og gerne vil have, at det tager sig pænt ud.

Markér bare en enkelt celle i skemaet. Vælg Formater - Autoformat. Vælg et design og klik OK:

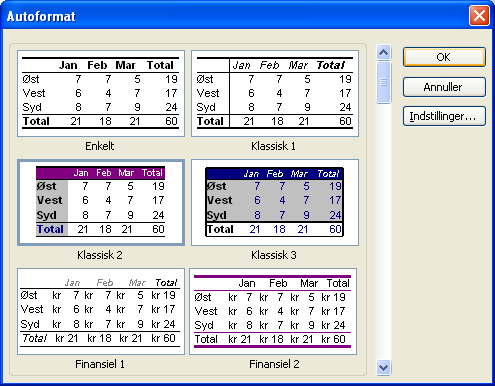
Så ser tabellen sådan ud:

Der er kommet farver og linjer på og alle kolonnebredder er tilpasset indholdet.

4. Indsæt formler - og skeln mellem relative og absolutte referencer

Nu skal vi omsider have regnearket til at regne. I de to nederste rækker skal vi have beregnet de relative ændringer for hvert kartoffelstykke. Det gør vi ved at konstruere en formel i celle D9 og derefter kopiere den til de øvrige celler.

Formler er det der for alvor gør et regneark anderledes end et tekstbehandlingsprogram. Formler kan indeholde:

• matematiske operatorer (+; addition, *; multiplikation o.s.v.)

• referencer til celler

• værdier (tal)

• de såkaldte regnearkfunktioner, som vi kommer til senere.

Når formler er indtastet - og er gyldige - vises de ikke i den celle de er indtastet i, men derimod vises den værdi den enkelte formel giver som output. Formler starter med tegnet =.

Den relative længdeændring i procent regnes ud som ((differensen mellem slut- og startlængde) divideret med startlængden) gange 100. Det kan indsættes som en formel enten

• ved at forbinde de nødvendige operatorer og betegnelser for cellerne eller lidt smartere 

• ved en udpegningsmetode, hvor vi i stedet for at skrive cellebetegnelser blot klikker på cellerne én efter én.

Marker celle D9. Skriv et lighedstegn. Sæt en startparentes, så vi først får udregnet differensen mellem start- og slutlængde. Klik i celle D7. Straks sættes cellebetegnelsen ind i formlen:

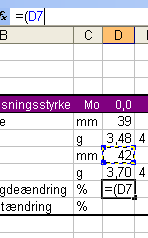
Fortsæt med at indtaste operatorer og parenteser til formlen er færdig:

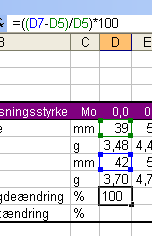
Klik til sidst på det grønne Indsæt-tegn til venstre for formellinjen, og straks vises i cellen formlens output:

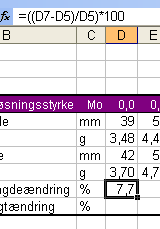
I stedet for nu at gennemføre den samme procedure i cellerne E9 - I9 kan vi blot kopiere formlen hørende til D9 og indsætte den i cellerne E9 til I9. Markér celle D9. Højreklik og vælg Kopier. Marker cellerne E9 til I9. Højreklik og vælg Sæt ind. Straks sætter programmet ensdannede formler ind og viser disse formlers output. Programmet "regner selv ud", at der til celle E9´s formel skal bruges værdierne fra cellerne E7 og E5 og ikke længere D7 og D5:

Tip! At programmet selv kan regne ud, at referencerne - betegnelserne for cellerne med værdier, der skal regnes på - skal ændres, når formlen kopieres over i nye felter, kræver, at referencerne i den celle formlen i første omgang indtastes i indtastes som såkaldt relative referencer. En relativ reference omfatter kun bogstavet for kolonne og tallet for række. 
Hvis du i en formel henviser til en bestemt værdi, der skal genbruges i uændret form i kopier af den oprindelige formel, så kan man skrive denne gennemgående værdi, f.eks. en omregningsfaktor eller en anden konstant størrelse, i en bestemt celle og så henvise til denne celle med en absolut reference. En absolut reference består af tegnet $ + bogstav for kolonne + $ + tal for række. 
Hvis en formel f.eks. lyder: =2*(L6-$K$2) er referencen til L6 relativ og referencen til K2 absolut. Hvis du kopierer formlen til andre celler vil referencen til L6 automatisk blive skiftet ud med en anden, mens referencen til K2 bevares.

Brug den samme eller en anden metode til at få sat formler ind, der beregner de relative vægtændringer.

Formatér til sidst cellerne, så procenttallene vises uden decimaler:

5. Brug funktioner

Funktioner kan beskrives som formler, der er forudprogrammerede i programmet. Funktionerne kan enten bruges som de er eller indsættes som delelementer i formler du selv konstruerer. Med funktioner kan du ofte spare tid i forhold til selv at skrive alle regnetrinnene ind i en formel, og dine formler kan blive enklere.

Funktioner kan enten indskrives direkte i formellinjen eller vælges fra lister over mulige funktioner. Det sidste er det mest brugte. Lad os sige, at vi vil have endnu en række i vores tabel med den gennemsnitlige relative ændring for hver af kartoffelstykkerne - altså middelværdien af den relative længdeændring og den relative vægtændring. I cellen under cellen med den relative vægtændring for kartoffelstykket i 0,0-opløsningen kunne vi konstruere formlen =(D9+D10)/2, som ville give os den søgte gennemsnitsværdi. Og så ville vi kunne kopiere dén formel til de sidste celler i rækken. Når det drejer sig om et gennemsnit af kun to værdier er det jo faktisk ikke så stort et arbejde, men hvis det nu drejede sig om et stort datasæt ville det være trivielt at skrive alle cellereferencerne op. Så for eksemplets skyld ser vi, hvordan det kan gøres endnu hurtigere med en funktion:

Markér cellen D11. Vælg Indsæt - Funktion:

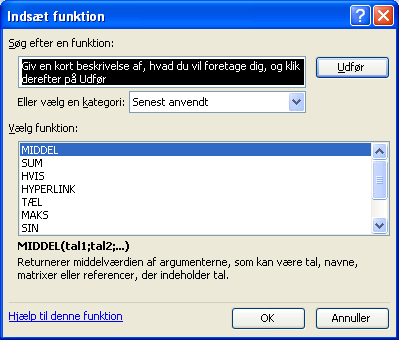
MIDDEL-funktionen er den først tilbudte, så du skal bare klikke på OK. Nu skal du vælge funktionens "argumenter": Argumenterne er de data du vil have funktionen udført på:

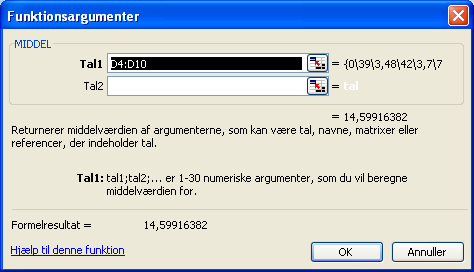
Du kan se, at programmet "gætter på", at du vil kende middelværdien af alle værdierne i D-kolonnen, så dét gæt skal lige korrigeres inden du klikker på OK. Ellers er det jo ikke kun de to ønskede værdier funktionen kigger på. Du kan blot ændre 4-tallet i den markerede boks til et 9-tal, men vi kan også benytte lejligheden til at introducere programmets celle-udpegningsværktøj. Det aktiveres ved at du klikker på den lille knap til højre for den med sort markerede boks. Nu klappes dialogboksen sammen, og knappen ved den markerede boks skifter udseende:

Udpeg med musemarkøren de to ønskede celler, D9 og D10, og klik på knappen ud for den rigtige celleidentifikation:

Nu kan du klikke på OK i Funktionsargumentdialogboksen, og så virker funktionen og udregner middelværdien af de relative ændringer:

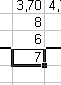
Den viser sig, ikke overraskende, at være 7.

Markér cellen med 7-tallet, kopiér og sæt ind i E11 - I11:

Flere funktioner

Hvis den ønskede funktion ikke findes blandt de umiddelbart tilbudte under Senest anvendte, kan du klikke på pilen i boksen og få en liste over en lang række yderligere kategorier, f.eks. til statistik:

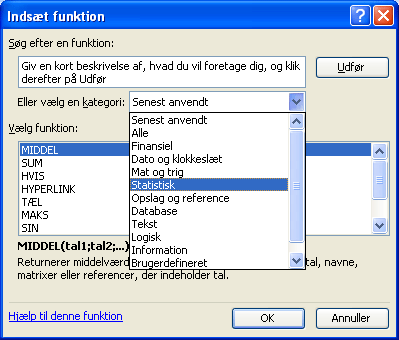
Bemærk, at den markerede funktion meget kort beskrives under listen med valgmuligheder. Her kan du se, hvad funktionen CHITEST "returnerer" (d.v.s. skriver) i det felt, hvor den indsættes:

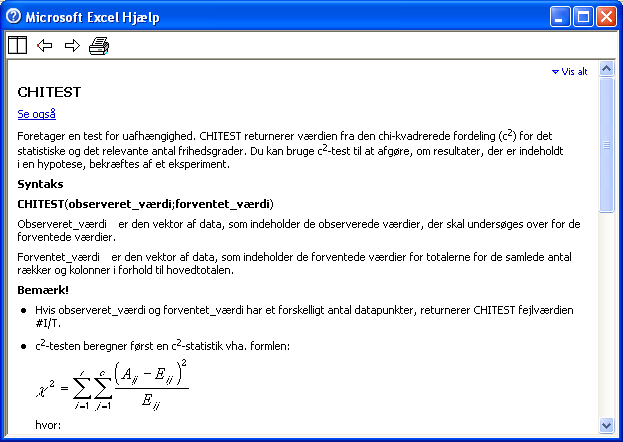
Mange funktioner er matematisk set temmelig avancerede og kan kun benyttes korrekt, hvis du faktisk er med på matematikken bag funktionen og dit datasæt er konstrueret og tilgængeligt i dit regneark på den måde funktionen foreskriver. F.eks. angiver en chi2-test således, hvor god overensstemmelse der er mellem et sæt beregnet forventede og et sæt faktisk observerede data. (Prøv funktionen i funktion i punkt 15 i denne vejledning). Flere oplysninger om den matematiske baggrund for den enkelte funktion kan du få ved at klikke på linket "Hjælp til denne funktion":

6. Sortér data

Excel kan ud over at regne, håndtere mange forskellige visninger af et sæt data. F.eks. kan data sorteres efter forskellige kriterier, alt efter hvad man er interesseret i at se efter.

Der er ikke megen mening i at sortere vores kartoffeldata efter andet end opløsningstyrken, så vi konstruerer en oversigt over en tænkt investeringsklub med seks medlemmer. Af tabellen kan man se, hvor de enkelte medlemmer bor, hvilket beløb de i 2003 har indbetalt og hvilket afkast de har opnået.

Hvis vi nu kunne tænke os en oversigt, hvor medlemmerne opstilles alfabetisk efter deres efternavn kan vi gøre det på denne måde:

Markér skemaets datafelter: 

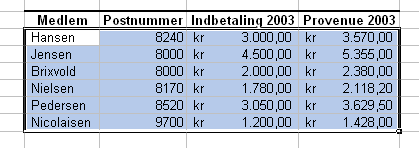
Klik på Data - Sorter. Bemærk, at programmet selv foreslår sortering efter Medlem. Programmet kan selvfølgelig kun foreslå denne betegnelse for sorteringsprincippet, fordi kolonnen omhyggeligt er benævnt i skemaet:

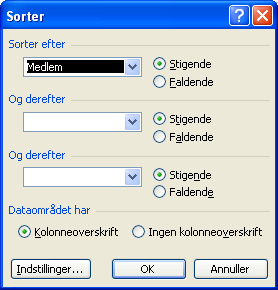
Klik på OK, og voila; skemaets rækker har byttet plads, så medlemmerne nu kommer i alfabetisk rækkefølge:

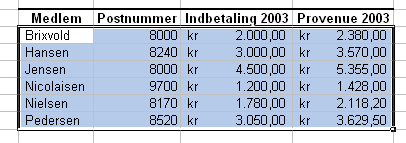
Hvis vi i stedet vil se oversigten, så medlemmerne opstilles efter, hvem af dem, der har haft det største provenue, skal - mens dataområdet stadig eller igen er markeret - kolonnen Provenue vælges som sorteringsprincip:

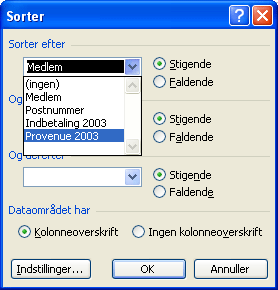
Igen viser det sig at være smart med benævnelsen i kolonnerne. Resultatet bliver nu dette:

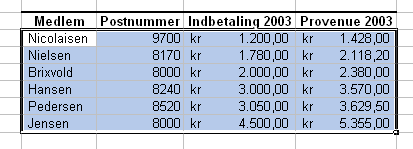
Hvordan skulle sorteringsrækkefølgen laves om, hvis medlemmet med størst provenue skulle stå øverst?

7. Lav enkle grafiske fremstillinger

Diagrammer er grafiske anskueliggørelser af taldata. Det kan være svært at aflæse tendenser, forskelle, ligheder o.s.v. i store talserier, og dét kan diagrammer gøre noget ved.

Vi vender tilbage til vores kartoffeldata.

Markér de data du vil have anskueliggjort: Vi skal have afbildet ændringerne som funktion af opløsningsstyrken, så vi markerer rækkerne 4, 9 og 10:

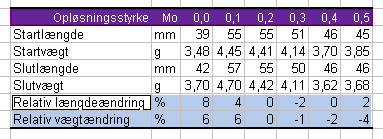
Start programmets Diagramguide: Indsæt - Diagram. Der er mange typer at vælge imellem, og hvilken der er den rigtige afhænger helt af den konkrete opgave, det konkrete formål med at lave et diagram. Her vil vi gerne se tendenser og vi vil gerne finde et skæringspunkt mellem bedte rette linje mellem punkterne i de to dataserier og x-aksen. Til det formål er Diagramtype "XY-punkt" og Undertype "Punktdiagram med datapunkter forbundet med kurver" bedst egnet:

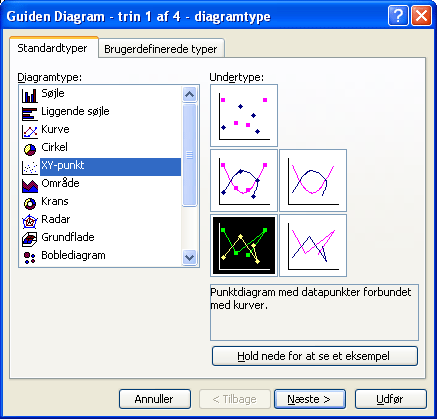
Klik på Næste. Det ser fornuftigt ud. Foretag ikke ændringer:

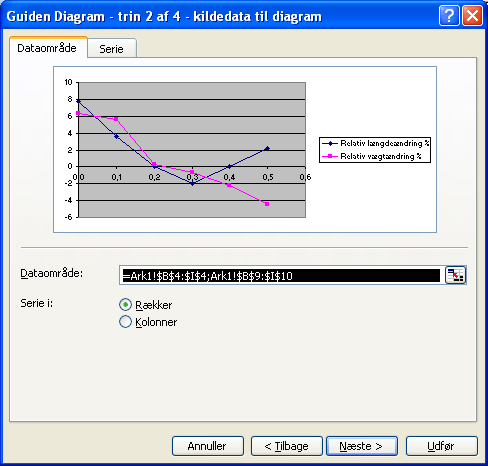
Klik på Næste igen. Indskriv en meningsfuld titel for grafen og betegnelser på akserne:

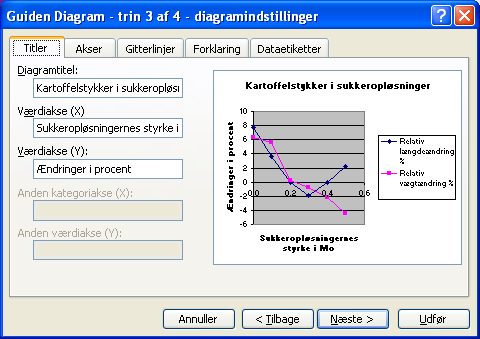
Der skal ikke ændres noget på de andre faneblade. Klik på Næste igen og klik på Udfør i Trin 4. Et diagram indsættes på siden med dit skema:

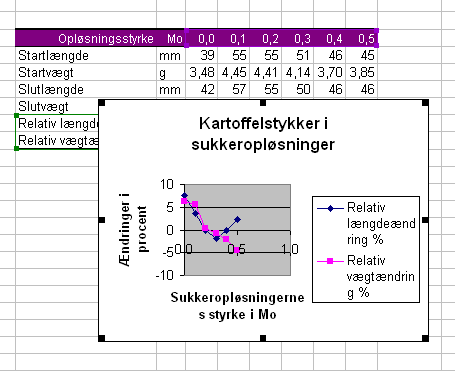
Du kan trække rammen større, så diagrammet bliver tydeligere at se. 

Du kan rette formateringen af teksterne til ved at klikke på tekstboksene, højreklikke og vælge Formater aksetitel.

Vi kan få programmet til at tegne den bedste rette linje gennem dataserierne én ad gangen ved at markere dataserien:

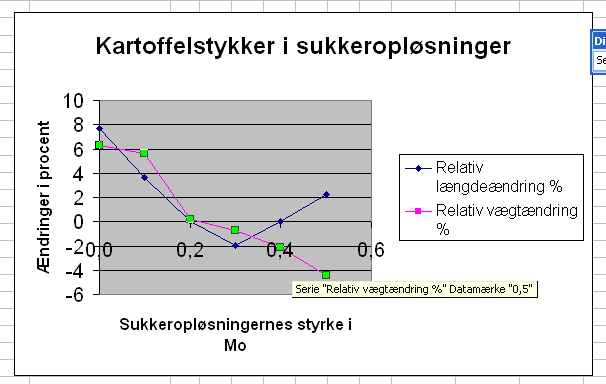
..., højreklikke og vælge Tilføj tendenslinje, Type Lineær:

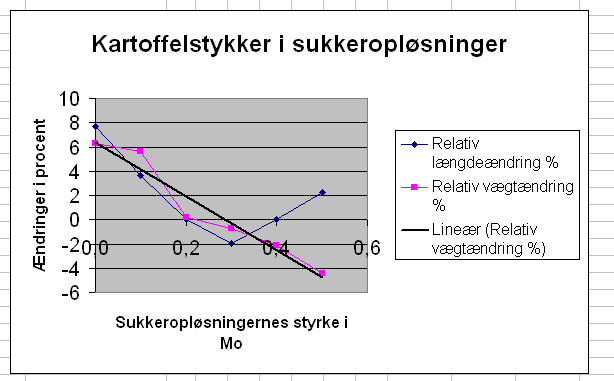
8 - 9 (Følger)

10. Integrer mellem Excel og Word

a. Fra Excel til Word

Det er let at flytte grafer og skemaer konstrueret i Excel over i et tekstbehandlingsdokument i Word.

Marker en graf ved at klikke inde på graffladen. Grafruden får markeringsfirkanter lige inden for rammen som tegn på, at den nu er det markerede objekt:

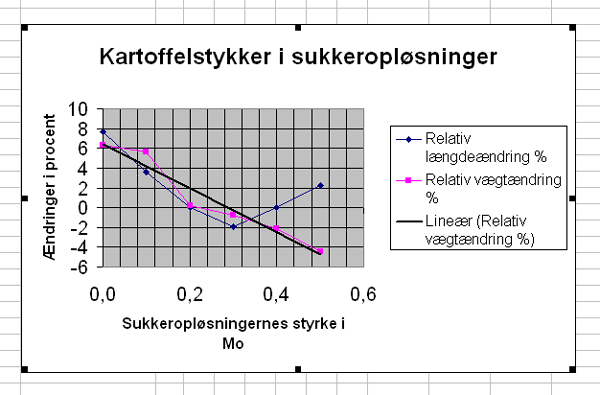
Tag en kopi af grafen og læg den i computerens udklipsholder. Højreklik og vælg Kopier eller tast Ctrl + C.

Åbn derefter et vindue med det tekstbehandlingsdokument, hvor du ønsker grafen indsat.

Placér cursoren hvor du vil have grafen indsat, højreklik og vælg Sæt ind eller tast Ctrl + V. Hvis du f.eks. vil have grafen lidt mindre i Worddokumentet kan du markere den dér og gribe fat i et hjørne og trække den mindre:

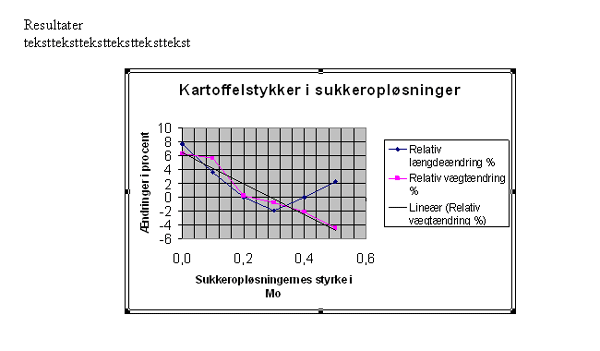
I Word fingerer den indsatte figur som en hvilken som helst anden indsat figur. Du kan ved at højreklikke på grafen få en figurvalgs-højreklikmenu frem og f.eks. vælge at skrive en figurtekst til grafen:

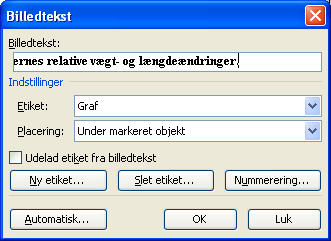
Som standard har Word etiketterne Figur, Ligning og Tabel. Hvis du har brug for flere, f.eks. "Graf" som her, kan du selv tilføje den etikettype ved at klikke på Ny etiket-knappen.

Når du har skrevet din figurtekst klikker du på OK og etiket, nr. og tekst sættes ind under figuren:

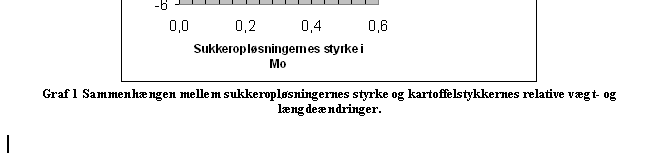
Du kan evt. tilpasse formateringen af teksten ved at markere den og ændre skrifttype etc. og ved at lave andre linjebrud med Enter:

Prøv selv at flytte en tabel fra Excel til Word.

Bemærk, at en tabel ikke i Word bliver indsat som et sammenhængende billede, der f.eks. kan forsynes med en billedtekst som grafen ovenfor. Til gengæld kan du i Word arbejde videre på formateringen af tabellens enkelte elementer, hvis du vil, eller lave enkelte ord eller tal til hyperlinks. Dén mulighed har du ikke med den overførte graf; den er ét sammenhængende billede, hvis enkeltdele ikke kan manipuleres hver for sig. Du kan f.eks. ikke skifte skrifttype på aksebetegnelserne eller stregfarve eller -tykkelse i Word-versionen. Hvis du vil lave noget om med dén slags, må du tilbage i Excel og gøre det på udgaven dér.

b. Fra Word til Excel

Måske kommer du ud for, at du i Word er begyndt på at opstille en tabel, og at du får brug for at lave nogle beregninger med tabellens værdier og/eller få tegnet en graf over nogle af værdierne. I det tilfælde kan du let kopiere tabellen eller dele af den over i Excel og fortsætte arbejdet dér. Det er ikke nødvendigt at lave et manuelt indtastningsarbejde forfra.

Vi forstiller os - meget enkelt - at vi har undersøgt nogle priser på brædder af forskellige træarter. Bræddernes længde er imidlertid forskellige, så vi kan ikke uden videre sammenligne priserne. Vi flytter vore rådata fra Word over til Excel for at regne på det dér. Tabellen markeres i Word:

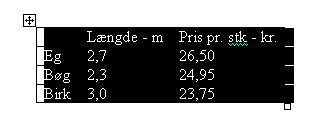
... og Copy-Pastes over i Excel:

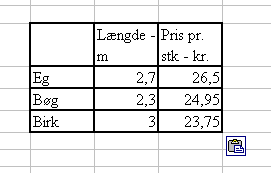
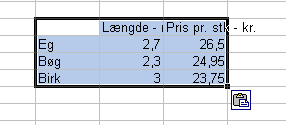
Du kan klikke på det lille Indsæt-fra-udklipsholderen-valgmuligheder-symbol og vælge Benyt samme formatering som destinationen - så tager det sig straks mere regnearksagtigt end tekstbehandlingsagtigt ud:

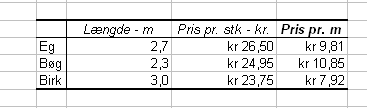
Nu kan du tilføje en kolonne til højre, "Pris pr. m", indsætte en formel i cellen ud for Eg, der beregner meterprisen, kopiere denne formel til de to øvrige celler, markere hele tabellen og bruge Autoformatfunktionen under Formater til at sætte den udvidede tabel pænt op:

11 - 14 (Følger)

15 Chi²-test

a. Introduktion og eksempelmateriale

En Chi²-test [ki i anden-test] er en matematisk analysemetode. Testen bruges til at afgøre, om et sæt observationer er så meget anderledes end et andet sæt observationer, at det er urealistisk, at afvigelsen blot skulle kunne være en tilfældighed. Med andre ord; om noget er signifikant anderledes end noget andet.

I samfundsfag kan vi f.eks. have indhøstet nogle stemmetal på nogle bestemte partigrupperinger (venstre-, midter- og højre-partier). Stemmetallene er opdelt på pigers og drenges stemmer, og vi kunne nu have lyst til at undersøge, om det passer, at der er forskel på pigers og drenges partivalg. Det er der nogen, der siger, at der er.

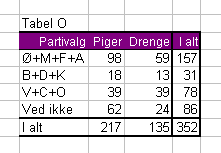
Rådataene har vi i denne tabel, som vi kalder Tabel O(bserveret):

Hvis vi kigger på partiblokken V+C+O passer påstanden tilsyneladende slet ikke. Der er 39 piger og 39 drenge, der har stemt på et af partierne i dén blok. Men, men: I alt var der jo flere piger end drenge, der stemte, så måske er der alligevel noget om, at der er forskel? Og er 98 mange nok flere end 59 til at man overhovedet kan sige, at der er større tilslutning til Ø+M+F+A-blokken blandt pigerne, når man tager i betragtning, at der i alt var flere piger end drenge, der stemte. Dén slags spørgsmål kan man diskutere i uendelige tider uden at komme nogen vegne - eller man kan bruge en chi²-test. Den kan give et klart svar på, hvor sikkert det er, at pigernes og drengenes stemmemønstre faktisk er forskellige.

Men hvad er det vi skal sammenligne med? Vi har jo kun dette ene sæt observationer. Her gør vi så det lille kunstgreb, at vi laver en tilsvarende tabel, men denne gang med nogle værdier, der svarer til, at der ikke er forskel på, hvordan de to køn stemmer. Vi kan på baggrund af fordelingen mellem piger og drenge og af regne ud, hvordan stemmetallene for de enkelte blokke skulle have været, hvis drenge og piger stemmer ens. 

F.eks. ville antallet af piger, der stemmer i Ø+M+F+A-blokken være givet ved dette udtryk: 

andelen af piger i hele gruppen x andelen af Ø+M+F+A-stemmere i hele gruppen x antallet af personer i hele gruppen

= 217/352 x 157/352 x 352

= 96,7893.

Da venstreorienterede piger selvfølgelig er hele mennesker runder vi op til 97 personer.

Efter dette forholdsregnings-princip kan en tabel som dem med de observerede stemmetal opbygges med de stemmetal, vi kunne forvente, hvis der ingen forskel var i pigers og drenges stemmemønster. Vi kalder den Tabel F(orventet).

Og når vi har de to tabeller har vi to sæt observationer, som kan sammenlignes i en chi2-test. Chi2-testen giver et tal for, hvor sandsynligt det er at forskellene mellem værdierne i tabel O og tabel F er rent tilfældige. Hvis det ikke kan udelukkes, at forskellene er tilfældige, så kan vi ikke sige, at drenge og piger stemmer forskelligt. Hvis chi2-testens resultat siger, at det med god sikkerhed kan udelukkes, at forskellene mellem O- og F-værdierne er tilfældige, så kan vi sige, at piger og drenge faktisk stemmer forskelligt og give os til at fundere over, hvordan dét kan være.

Signifikans
Chi²-testen beregner, populært sagt, forskellen talpar for talpar (O-værdi sammenlignet med F-værdi) og lægger forskellene sammen. En høj chi²-værdi tyder derfor på stor afvigelse mellem det forventede og det observerede. Når man laver en chi²-test i Excel er det imidlertid ikke chi²-værdien selv, man får som output at vurdere på, men en såkaldt p-værdi (af engelsk propability - sandsynlighed). Bemærk, at p-værdien er lav, hvis chi²-værdien er høj! D.v.s.: jo lavere p-værdi, desto større sandsynlighed for, at forskellen er signifikant - altså ikke er tilfældig.

• Hvis p = 0,05 er der 95% sandsynlighed for, at forskellen mellem det observerede og det forventede er signifikant.

• Hvis p = 0,01 er der 99% sandsynlighed for, at forskellen mellem det observerede og det forventede er signifikant.

Det er almindeligt, at man beslutter, at arbejde med et "signifikansniveau" på 95%. Det vil sige, at man kalder alle afvigelser mellem datasæt med p-værdier på under 0.05 for signifikante. Men begrundelserne herfor har med fagtraditioner, statistiske antagelser og sandsynlighedsregning at gøre, så det vil vi ikke beskæftige os mere med lige i denne Excel-vejledning.

b. Chi²-test i Excel

Lad os sætte O- og F-tabellerne op og gennemføre selve testen i Excel. Nu vil vi altså have fundet ud af, om drenge og piger stemmer forskelligt eller ej.

Først opretter vi en simpel tabel med vore observerede data. Tallet 352 skal stå i celle E9, hvis du direkte vil kunne sammenligne med formlerne i det nedenstående.

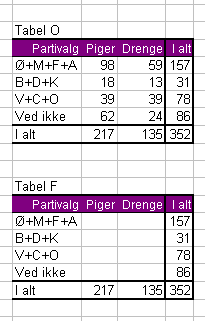
Så tager vi en kopi af denne tabel, sætter kopien ind nedenunder, sletter i kopien de 8 stemmetal inde i tabellen og kalder kopien Tabel F. Tabel F´s 352 skal stå i celle E18, hvis du direkte vil kunne sammenligne med formlerne i det nedenstående:

Nu skal vi i de otte felter indsætte formler, der beregner de forventede stemmetal. Vi starter i feltet med piger, der stemmer Ø, M, F eller A. Her bruges udtrykket vi kom frem til i afsnit 15a:

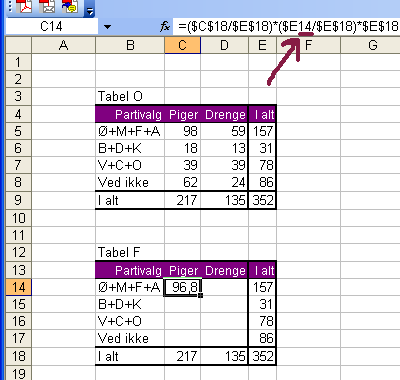
Bemærk, at vi for at få denne formel til at virke, så den kan kopieres til de tre andre pige-felter, er nødt til at bruge absolutte cellereferencer (se evt. tippet i punkt 4 i denne vejledning) . Kun ét sted skal der ikke dollartegn foran: ved referencen til cellen med angivelsen af rækkenummeret for Ø+M+F+A-blokken; 14 (ved den røde pil herover). Vi vil jo opnå, at denne reference kan skifte til hhv. række 15, 16 og 17, når vi kopierer formlen ind i cellerne under C14.

Kopiér formlen ind i felterne under C14, ændr decimalantallet til 0 for alle de otte celler (hele mennesker) og konstruer en formel, der beregner de forventede drengevælgertal og kopier den til alle felter:

Nu har du en Tabel O med de observerede tal og en Tabel F med nogle konstruerede "forventede" tal. Nu kan du sammenligne disse tal og få en p-værdi, der siger, hvor sandsynligt det er, at forskellene er små nok til at de er tilfældige.

Vælg en celle og skriv teksten "p-værdi=".

Markér cellen derunder. Det bliver i denne celle outputtet af din chi²-test - p-værdien - kommer til at stå. Klik på funktionsknappen "fx" oppe ved formellinjen eller vælg Indsæt - Funktion. Vælg Kategori Statistik og funktionen CHITEST:

Tryk OK og vælg de 8 celler i Tabel O som funktionsværdier til observerede værdier og de 8 celler som funktionsværdier til forventede værdier:

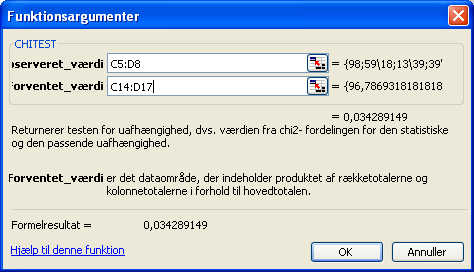
Tryk på OK og du får din p-værdi ud i den valgte celle:

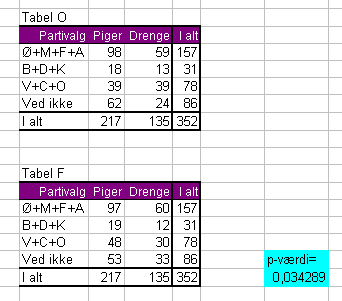
Der er altså knapt 97% sikkerhed for, at der er forskel på, hvordan piger og drenge stemmer.

Hvis vi arbejder med et signifikansniveau på 95% vil vi nu kunne sige, at vores beregning viser, at der faktisk er forskel på, hvordan piger og drenge stemmer.

Tilbage til vejledningens forside